What exactly is a monthly mean?
According to recent reports (see CNN & The Australian) it appears that the speed of the Greenland ice melt has been increasing at an 'alarming' rate...
The trouble with this is that this is only a problem if:
- The measurements are indeed accurate enough to allow this analysis to stand, and,
- The melt water remains as melt water and is not taken up by other parts of the climatic system (i.e. it gets converted back to ice somewhere else) and remains in balance as a whole.
Now, look at the following:
Embracing Data 'Noise' Brings Greenland's Complex Ice Melt Into Focus
To quote:
"An enhanced approach to capturing changes on Earth's surface via satellite could provide a more accurate account of how ice sheets, river basins and other geographic areas are changing as a result of natural and human factors. In a first application, the technique revealed sharper-than-ever details about Greenland's massive ice sheet, including that the rate at which it is melting might be accelerating more slowly than predicted."
Basically a way has been found of 'cleaning up' the satellite data to give us a more accurate picture of the rate of ice melt. again to quote:
"In addition, the enhanced detail of where and how much ice melted allowed the researchers to estimate that the annual acceleration in ice loss is much lower than previous research has suggested, roughly increasing by 8 billion tons every year. Previous estimates were as high as 30 billion tons more per year."
I think you will agree that is some difference between 30 billion and 8 billion tones a year.
How much is a billion tones of water?
One 1000 litres or kg's of water is a ton, that takes up one cubic meter. Therefore a thousand by a thousand by 1 meter square of water is one million tones. Go up another 1000 meters so you have a 1000 meter by 1000 meter by 1000 meter cube and that is equal to 1 billion tones (water is heavy!).
Now the surface area of the Earth is 510 million square kilometers. So if we take the millimetre 'height' of our 1km cube (i.e. 1 million millimetres) and divide that by the Earth's surface area we get how much 1 billion tones of water increases surface height if equally spread across the planet, which is easy, its 1/510 of a millimetre or 0.0019 mm.
So 1 billion tones water EQUALS 0.0019 mm of surface height increase.
Basically, what is everybody getting so worried about???
Water freezes..
Now you can't just look at Greenland and its ice melt without considering places where the ice is freezing. Have a look the graph below of Antarctic Sea Ice Extent.
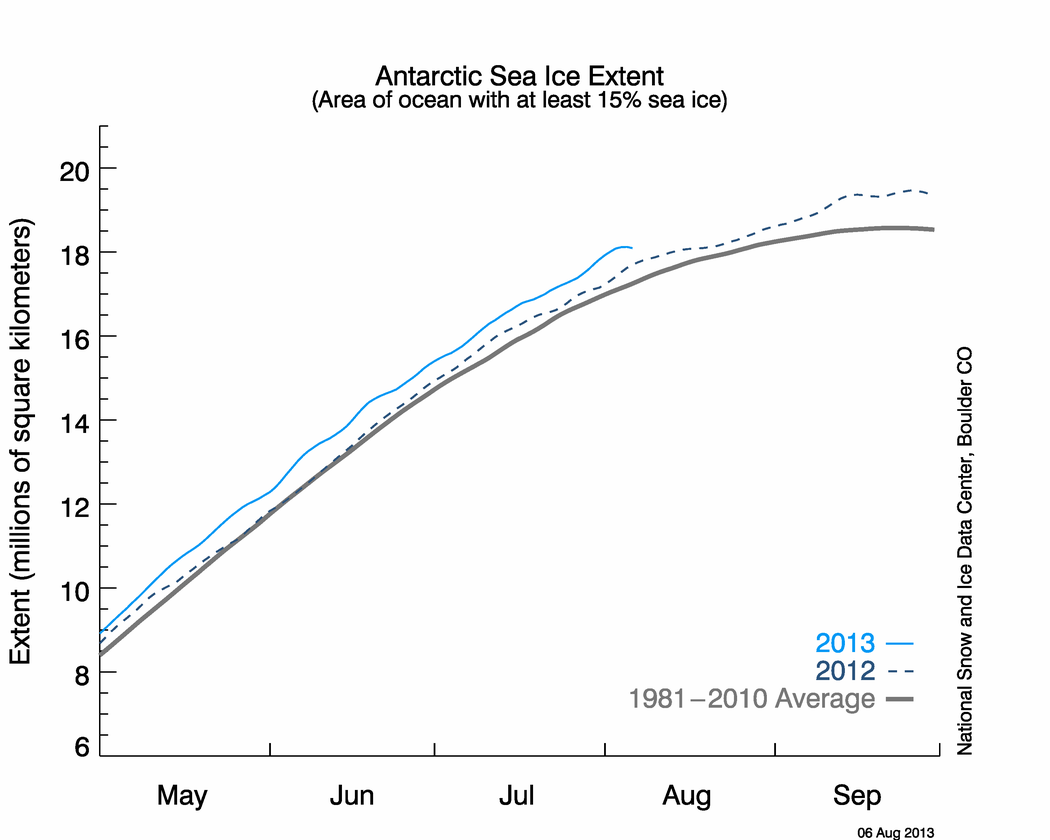
Notice something strange? Yes, the Antarctic has accumulated well over a million square kilometers of sea ice above the average. Now even if that ice was just 1cm deep (likely to be far deeper in the places where it is covered, but this makes for simple maths) then that equals 10 1km cubes of water or 10 billion tones of water...
See how utterly daft it is to consider what happens in one part of the environment without the other parts? Also this points out how important it is to have accurate measurements.
Follow us on Facebook, click here!

Comments left
- Steven Mosher said:
There are several reasons why your derived value can be different from that given in GHCN.
1. Application of a TOBS correction in ghcn. which ghcn file are you using?
2. Averaging of duplicates in the ghcn file. for example if there are two instruments at the same location then GHCN will average these.
3. To calculate a monthly mean ghcn does this:
a. They take the daily min and daily max as defined by ( I believe ) a midnight time of observation. this is important and can cause differences.
b. The min figure is rounded. the max figure is rounded ( nearest F)
c. day ave = min+max/2. rounded. i believe, have to check the manual.
d. days are summed to the month
In general in studying hundreds of stations over decades you will find a difference between the "hourly" average and min/max average. But you wont find a trend bias, which is what matters.ON Fri, 23 Apr 10, 4:43am probably from United States Reply to this comment
- Eco Guy said:
In answer,
ftp://ftp.ncdc.noaa.gov/pub/data/ghcn/v2/v2.mean.Z as downloaded on 21st Jan 10 for GIS model. not the _adj version. I have a ref to TOBS. I'll also try with the adjusted data.
anyway to find out if they had multiple instruments at a location?
wow on rounding the intermediate min/max - any reason given? Also do they define the rounding being done, i.e. nearest, up, down, 5up etc.
Yep, there probably won't be a trend to see, but I'm actually more interested in the effect on confidence this introduces and if that varies over the months and temp ranges encountered. Easy enough for me to put in a DB and check, although wondering if this has been done before.ON Fri, 23 Apr 10, 8:45am probably from Australia Reply to this comment
- Eco Guy said:
Got a question or comment about this?
Find what you were looking for?.. Not quite what you expected?.. Got a question to ask people?Share your thoughts and use the form below to post a public comment right on this page.